はじめに
量子力学に関する話では
- 重ね合わせ
- 量子が二つの状態をとる
などはキーワードとしてよく耳にします。などなどを耳にしたことがあるかと思います。
一方で直感に反するこの概念を分かった気になるためには『確率波』という日常生活では想像もつかない事象を理解する必要があります。
というわけで、本記事ではそれらについて”分かった気になる”ところをゴールにし、正確性を犠牲にして平易な文章で記載してました。
確率波を理解する
鏡と位相
まず登場するのは、2種類の鏡である半透鏡と鏡(全反射)です。

それぞれの鏡に入射する光は位相のずれが発生しますが、それらが1/2,1/4と位相がずれた際のイメージは以下です。
ポイントは一つの波が半波長分(1/2分)ずれた場合、元の波と合成すれば山の位置が逆転していることから分かる通り、重ね合いによって波は消えてしまいます。
鏡を用いた位相の実験
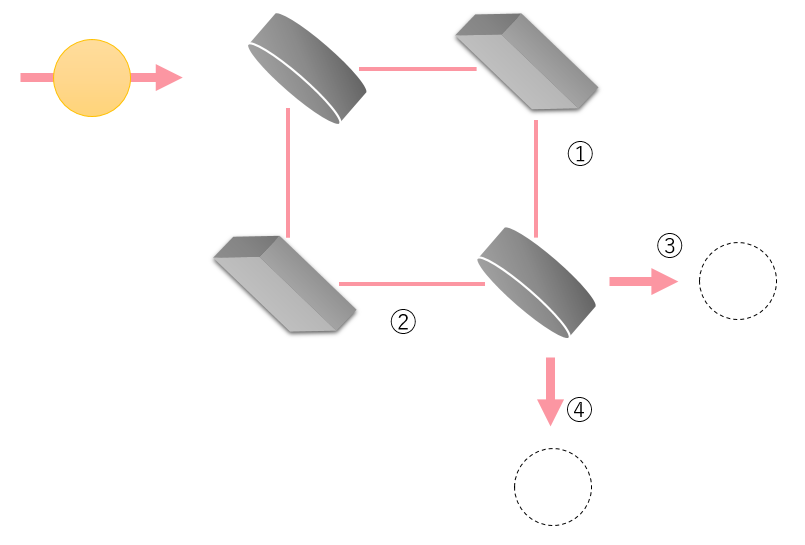
2つの半透鏡と2つの鏡を下記のように配置し、レーザーポインタ(光子の集まり)で光を投入すると③と④から光がでてきます。

そして出てくる光は半透鏡と鏡の位置を調整すれば、全ての光を③から出すことも可能です。具体的には経路①と経路②の距離を全く同じにすることで④から光は出てこずに全て③から光が出てきます。
この理由は位相差にあります。
経路①を通って2つ目の半透鏡に進入する光は”半透鏡で透過+鏡で反射”され、②を通る光は”半透鏡で反射+鏡で反射”されます。そして、経路①を通った光が③にでてくるのは"半透鏡で透過+鏡で反射+半透鏡で反射"、経路②を通った光が③に出てくるのは"半透鏡で反射+鏡で反射+半透鏡で透過"ということで、順番は違うも最終的には位相は揃うので分かれた光が強めあう形となります。
一方で④にでてくる光は、経路①を通った光が③にでてくるのは"半透鏡で透過+鏡で反射+半透鏡で透過"、経路②を通った光が④に出てくるのは"半透鏡で反射+鏡で反射+半透鏡で反射"されるので、③とは違って片方の経路は半透鏡で2回反射しているので1/2 波長分位相がずれています。よって、④からは光が検出されない、というロジックです。
逆に①の経路を1/2波長分長くしたりすると同じロジックで③から光が検出されずに④からのみ光が出てきます。
本題
レーザー(光子の集まり)ではなく光子1粒だけ入れるとどうなるのでしょうか。
まず前提として光子1粒をそのまま半透鏡に入れると、ランダムに透過/反射が50%の確率で起こります。

さて、先ほどと同じように配置した2つの半透鏡と2つの鏡に光子を入れるとどうなるでしょうか。

直感的には上図のように半透鏡でランダムに透過/反射を行いながら矢印の先で1/2の確率で検出できそうな気がしますが、実際は、レーザーを入れた時と同じ事象が起きます。
つまり二つの経路(先の図でいう①、②)を一致させれば100%③で検出されます。
これは「光子はなぜ二つの経路差を知っているのか」という直感に反する疑問にぶつかり、光子が二手に分かれているように見えます。これは、光子が波の性質を持っていることによって一粒の光子は一つ目の半透鏡を1/2の確率波という光子で透過&1/2の確率波という光子で反射されているという、二つの確率波の重ね合わせ状態になっていると考えると辻褄があう実験結果となっています。
終わりに
確率波のおもしろさ、奇妙さが満載の同実験ですが、以下の本にはより詳細が記載されています。
興味があれば、手にとってみてください。
